Summer Undergrad 2020 - Numerical Methods

Collection Number C20028

Collection Date May 24, 2020 - June 04, 2020

Collection Type Course

Displaying 1 - 5 of 5

Aaron Szasz Perimeter Institute for Theoretical Physics

May 26, 2020 Summer Undergrad 2020 - Numerical Methods

Talk Number PIRSA:20050040

Aaron Szasz Perimeter Institute for Theoretical Physics

May 28, 2020 Summer Undergrad 2020 - Numerical Methods

Talk Number PIRSA:20050041

Aaron Szasz Perimeter Institute for Theoretical Physics

June 01, 2020 Summer Undergrad 2020 - Numerical Methods

Talk Number PIRSA:20060011

Aaron Szasz Perimeter Institute for Theoretical Physics

June 03, 2020 Summer Undergrad 2020 - Numerical Methods

Talk Number PIRSA:20060012

Aaron Szasz Perimeter Institute for Theoretical Physics

June 05, 2020 Summer Undergrad 2020 - Numerical Methods

Talk Number PIRSA:20060013

Title	Speaker(s)	Date	Talk Type	Link to Content
Summer Undergrad 2020 - Numerical Methods (A) - Lecture 1	Aaron Szasz	2020-05-26	Course	View details
Summer Undergrad 2020 - Numerical Methods (A) - Lecture 2	Aaron Szasz	2020-05-28	Course	View details
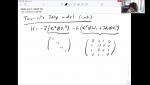
Summer Undergrad 2020 - Numerical Methods (A) - Lecture 3	Aaron Szasz	2020-06-01	Course	View details
Summer Undergrad 2020 - Numerical Methods (A) - Lecture 4	Aaron Szasz	2020-06-03	Course	View details
Summer Undergrad 2020 - Numerical Methods (A) - Lecture 5	Aaron Szasz	2020-06-05	Course	View details