
Time variation of fundamental constants and the Oklo phenomenon
Justin Torgerson Los Alamos National Laboratory
Search results

Justin Torgerson Los Alamos National Laboratory

Neal Weiner New York University (NYU)

Rishi Khatri University of Illinois Urbana-Champaign

Thomas Dent Max Planck Institute for Gravitational Physics - Albert Einstein Institute (AEI)

John Donoghue University of Massachusetts Amherst


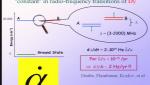
Dmitry Budker University of California, Berkeley

Julian King University of New South Wales (UNSW)

Jan Thomsen University of Copenhagen

James Bergquist National Institute of Standards & Technology

Michael Tobar University of Western Australia