Talks by Jeongwan Haah
-
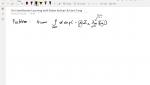
Time-efficient learning of quantum Hamiltonians from high-temperature Gibbs states
Jeongwan Haah Massachusetts Institute of Technology (MIT) - Department of Physics
-

Long-range entangled many-body states
Jeongwan Haah Massachusetts Institute of Technology (MIT) - Department of Physics
-

An invariant of topologically ordered states under local unitary transformations
Jeongwan Haah Massachusetts Institute of Technology (MIT) - Department of Physics
-

Demonstration of Self-correcting Quantum Memory in Three Dimensions
Jeongwan Haah Massachusetts Institute of Technology (MIT) - Department of Physics