
How to Make Testable Multiverse Theories
Lee Smolin Perimeter Institute for Theoretical Physics

Lee Smolin Perimeter Institute for Theoretical Physics

Mark Wyman PDT Partners LLC
Niayesh Afshordi University of Waterloo

Andreas Albrecht University of California, Davis

Mark Wyman PDT Partners LLC
Niayesh Afshordi University of Waterloo

Hilary Greaves University of Oxford

Gordon Kane University of Michigan–Ann Arbor

Tom Banks Rutgers University

Rudy Vaas University of Giessen
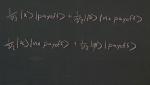
David Albert Columbia University

Laura Mersini-Houghton University of North Carolina at Chapel Hill

Peng Gao ExodusPoint Capital