
Entanglement and mixture in algebraic quantum field theory
Vincent Lam University of Queensland

Vincent Lam University of Queensland

Tim Ralph University of Queensland

Jaume Gomis Perimeter Institute for Theoretical Physics


Joan Vaccaro Griffith University
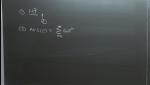
Carl Bender Washington University in St. Louis

Robert Spekkens Perimeter Institute for Theoretical Physics

Nate Bode California Institute of Technology

