
Model-Independent Constraints on Inflation from the CMB
Cora Dvorkin Harvard University

Cora Dvorkin Harvard University



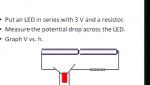

Richard Epp University of Waterloo

Richard Epp University of Waterloo