
Gravitational Physics - Review (PHYS 636) - Lecture 8
Ruth Gregory King's College London

Ruth Gregory King's College London

Susan Coppersmith University of Wisconsin–Madison

Xiao-Gang Wen Massachusetts Institute of Technology (MIT) - Department of Physics

Ruth Gregory King's College London
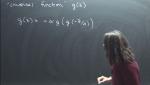
Susan Coppersmith University of Wisconsin–Madison
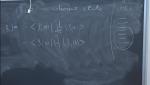
Xiao-Gang Wen Massachusetts Institute of Technology (MIT) - Department of Physics

Ruth Gregory King's College London

Susan Coppersmith University of Wisconsin–Madison

Xiao-Gang Wen Massachusetts Institute of Technology (MIT) - Department of Physics

Ruth Gregory King's College London

Susan Coppersmith University of Wisconsin–Madison

Xiao-Gang Wen Massachusetts Institute of Technology (MIT) - Department of Physics