
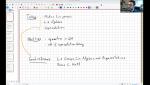
The Weak Gravity Conjecture, Naturalness, and Discrete Gauge Symmetries
Isabel Garcia Garcia University of Washington
Search results

Isabel Garcia Garcia University of Washington
Alioscia Hamma University of Naples Federico II
Aaron Szasz Alphabet (United States)

Theo Johnson-Freyd Dalhousie University

Dan Wohns Perimeter Institute for Theoretical Physics

Alioscia Hamma University of Naples Federico II

Nitu Kitchloo Johns Hopkins University

Aaron Szasz Alphabet (United States)

Yannick Herfray Université de Tours

Hang Yu California Institute of Technology (Caltech) - Division of Physics Mathematics & Astronomy