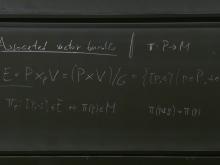Mathematical physics, including mathematics, is a research area where novel mathematical techniques are invented to tackle problems in physics, and where novel mathematical ideas find an elegant physical realization. Historically, it would have been impossible to distinguish between theoretical physics and pure mathematics. Often spectacular advances were seen with the concurrent development of new ideas and fields in both mathematics and physics. Here one might note Newton's invention of modern calculus to advance the understanding of mechanics and gravitation. In the twentieth century, quantum theory was developed almost simultaneously with a variety of mathematical fields, including linear algebra, the spectral theory of operators and functional analysis. This fruitful partnership continues today with, for example, the discovery of remarkable connections between gauge theories and string theories from physics and geometry and topology in mathematics.
Format results
-
13 talks-Collection NumberC25007
Talk
-

Lecture - Mathematical Physics, PHYS 777
Kevin Costello Perimeter Institute for Theoretical Physics
-

Lecture - Mathematical Physics, PHYS 777
Mykola Semenyakin Perimeter Institute for Theoretical Physics
-

Lecture - Mathematical Physics, PHYS 777
Kevin Costello Perimeter Institute for Theoretical Physics
-

Lecture - Mathematical Physics, PHYS 777
Kevin Costello Perimeter Institute for Theoretical Physics
-

Lecture - Mathematical Physics, PHYS 777
Kevin Costello Perimeter Institute for Theoretical Physics
-

Lecture - Mathematical Physics, PHYS 777
Kevin Costello Perimeter Institute for Theoretical Physics
-

Lecture - Mathematical Physics, PHYS 777
Kevin Costello Perimeter Institute for Theoretical Physics
-

Lecture - Mathematical Physics, PHYS 777
Kevin Costello Perimeter Institute for Theoretical Physics
-
-
Mathematical Physics (Core), PHYS 777-, January 6 - February 5, 2025
13 talks-Collection NumberC25002Talk
-

Lecture - Mathematical Physics, PHYS 777-
Mykola Semenyakin Perimeter Institute for Theoretical Physics
-

Lecture - Mathematical Physics, PHYS 777-
Mykola Semenyakin Perimeter Institute for Theoretical Physics
-

Lecture - Mathematical Physics, PHYS 777-
Mykola Semenyakin Perimeter Institute for Theoretical Physics
-

Lecture - Mathematical Physics, PHYS 777-
Mykola Semenyakin Perimeter Institute for Theoretical Physics
-

Lecture - Mathematical Physics, PHYS 777-
Mykola Semenyakin Perimeter Institute for Theoretical Physics
-

Lecture - Mathematical Physics, PHYS 777-
Mykola Semenyakin Perimeter Institute for Theoretical Physics
-

Lecture - Mathematical Physics, PHYS 777-
Mykola Semenyakin Perimeter Institute for Theoretical Physics
-

Lecture - Mathematical Physics, PHYS 777-
Mykola Semenyakin Perimeter Institute for Theoretical Physics
-
-
Classical Physics (Core), PHYS 776, September 3 - October 4, 2024
15 talks-Collection NumberC24031Talk
-

Lecture - Classical Physics, PHYS 776
Aldo Riello Perimeter Institute for Theoretical Physics
PIRSA:24090001 -

Lecture - Classical Physics, PHYS 776
Aldo Riello Perimeter Institute for Theoretical Physics
PIRSA:24090002 -

Lecture - Classical Physics, PHYS 776
Aldo Riello Perimeter Institute for Theoretical Physics
PIRSA:24090003 -

Lecture - Classical Physics, PHYS 776
Aldo Riello Perimeter Institute for Theoretical Physics
PIRSA:24090004 -

Lecture - Classical Physics, PHYS 776
Aldo Riello Perimeter Institute for Theoretical Physics
PIRSA:24090005 -

Lecture - Classical Physics, PHYS 776
Aldo Riello Perimeter Institute for Theoretical Physics
PIRSA:24090006 -

Lecture - Classical Physics, PHYS 776
Aldo Riello Perimeter Institute for Theoretical Physics
PIRSA:24090007 -

Lecture - Classical Physics, PHYS 776
Aldo Riello Perimeter Institute for Theoretical Physics
PIRSA:24090008
-
-
Mathematical Physics 2023/24
13 talks-Collection NumberC24026Talk
-

Mathematical Physics Lecture
Kevin Costello Perimeter Institute for Theoretical Physics
-

Mathematical Physics Lecture
Kevin Costello Perimeter Institute for Theoretical Physics
-

Mathematical Physics Lecture
Kevin Costello Perimeter Institute for Theoretical Physics
-

Mathematical Physics Lecture
Kevin Costello Perimeter Institute for Theoretical Physics
-

Mathematical Physics Lecture
Kevin Costello Perimeter Institute for Theoretical Physics
-

Mathematical Physics Lecture
Kevin Costello Perimeter Institute for Theoretical Physics
-

Mathematical Physics Lecture
Kevin Costello Perimeter Institute for Theoretical Physics
-

Mathematical Physics Lecture
Kevin Costello Perimeter Institute for Theoretical Physics
-
-
Higher Categorical Tools for Quantum Phases of Matter
15 talks-Collection NumberC24016Talk
-

-

Analogies between QFT and lattice systems
Anton Kapustin California Institute of Technology (Caltech) - Division of Physics Mathematics & Astronomy
-

Models of anyons with symmetry: a bulk-boundary correspondence
Fiona Burnell University of Minnesota
-

Twisted Tools for (Untwisted) Quantum Field Theory
Justin Kulp Stony Brook University
-

Quantum double models and Dijkgraaf-Witten theory with defects
Catherine Meusburger -

Topological sectors in quantum lattice models
Clement Delcamp Institut des Hautes Etudes Scientifiques (IHES)
-

Douglas-Reutter 4d TQFT as a generalised orbifold
Vincentas Mulevičius Vilnius University
-

Weak Hopf symmetric tensor networks
Andras Molnar University of Vienna
-
-
Quantum Field Theory for Cosmology (PHYS785/AMATH872)
24 talks-Collection NumberC24003Talk
-

Quantum Field Theory for Cosmology - Lecture 20240109
Achim Kempf University of Waterloo
-
Quantum Field Theory for Cosmology - Lecture 20240111
Achim Kempf University of Waterloo
-

Quantum Field Theory for Cosmology - Lecture 20240116
Achim Kempf University of Waterloo
-

Quantum Field Theory for Cosmology - Lecture 20240118
Achim Kempf University of Waterloo
-

Quantum Field Theory for Cosmology - Lecture 20240123
Achim Kempf University of Waterloo
-

Quantum Field Theory for Cosmology - Lecture 20240125
Achim Kempf University of Waterloo
-

Quantum Field Theory for Cosmology - Lecture 20240130
Achim Kempf University of Waterloo
-

Quantum Field Theory for Cosmology - Lecture 20240201
Achim Kempf University of Waterloo
-
-
Mathematical Physics - Core 2023/24
12 talks-Collection NumberC24005Talk
-
Twisted Holography Mini-Course
6 talks-Collection NumberC23050Talk
-

Twisted Holography Mini-Course - Lecture 20231102
Kevin Costello Perimeter Institute for Theoretical Physics
-

Twisted Holography Mini-Course - Lecture 20231109
Kevin Costello Perimeter Institute for Theoretical Physics
-

Twisted Holography Mini-Course - Lecture 20231116
Kevin Costello Perimeter Institute for Theoretical Physics
-

Twisted Holography Mini-Course - Lecture 20231123
Davide Gaiotto Perimeter Institute for Theoretical Physics
-

Twisted Holography Mini-Course - Lecture 20231130
Davide Gaiotto Perimeter Institute for Theoretical Physics
-
Twisted Holography Mini-Course - Lecture 20231214
Davide Gaiotto Perimeter Institute for Theoretical Physics
-
-
Topological Quantum Field Theories - mini-course
9 talks-Collection NumberC23048Talk
-

Topological Quantum Field Theories Lecture 20231006
Lukas Mueller Perimeter Institute for Theoretical Physics
-

Topological Quantum Field Theories Lecture 20231013
Lukas Mueller Perimeter Institute for Theoretical Physics
-

Topological Quantum Field Theories Lecture 20231020
Lukas Mueller Perimeter Institute for Theoretical Physics
-

Topological Quantum Field Theories Lecture 20231027
Lukas Mueller Perimeter Institute for Theoretical Physics
-

Topological Quantum Field Theories Lecture 20231103
Lukas Mueller Perimeter Institute for Theoretical Physics
-

Topological Quantum Field Theories Lecture 20231110
Lukas Mueller Perimeter Institute for Theoretical Physics
-

Topological Quantum Field Theories Lecture 20231124
Lukas Mueller Perimeter Institute for Theoretical Physics
-

Topological Quantum Field Theories Lecture 20231201
Lukas Mueller Perimeter Institute for Theoretical Physics
-
-
QFT for Mathematicians 2022
28 talks-Collection NumberC22011Talk
-

Welcome and Opening Remarks
Kevin Costello Perimeter Institute for Theoretical Physics
-

3d Theories and Twists I
Kevin Costello Perimeter Institute for Theoretical Physics
-

3d Gauge Theory and Elliptic Stable Envelopes I
Andrei Okounkov Columbia University
-

Classical BV Formalism and Topological Quantum Field Theory
Philsang Yoo Seoul National University
-

-
3d B Models and Knot Homology I
Lev Rozansky University of North Carolina at Chapel Hill
-

On Boundary VOA's
Davide Gaiotto Perimeter Institute for Theoretical Physics
-

3d Gauge Theory and Elliptic Stable Envelopes II
Mykola Dedushenko Stony Brook University
-
-
Global Categorical Symmetries
34 talks-Collection NumberC22008Talk
-

Welcome and Opening Remarks
Theo Johnson-Freyd Dalhousie University
-

Non-Invertible Symmetries in d>2
Justin Kaidi Stony Brook University
-
Monodromy and derived equivalences
Andrei Okounkov Columbia University
-

Lessons from SU(N) Seiberg-Witten Geometry
Emily Nardoni University of Tokyo
-

Vertex algebras and self-dual Yang-Mills theory
Kevin Costello Perimeter Institute for Theoretical Physics
-

Non-invertible Global Symmetries in the Standard Model
Shu-Heng Shao Stony Brook University
-

Analytic Langlands correspondence over C and R
Pavel Etingof Massachusetts Institute of Technology (MIT)
-

A (kind of) monoidal localization theorem for the small quantum group
Cris Negron University of Southern California
-
-
Women at the Intersection of Mathematics and Theoretical Physics
16 talks-Collection NumberC21002Talk
-

Welcome and Opening Remarks
-
Bianca Dittrich Perimeter Institute for Theoretical Physics
-
Theo Johnson-Freyd Dalhousie University
-
Sylvie Paycha University of Potsdam
-
Katarzyna Rejzner University of York
-
Anne Taormina Durham University
-
Reiko Toriumi Okinawa Institute of Science and Technology Graduate University
-
-

Division algebraic symmetry breaking
Cohl Furey Humboldt University of Berlin
-

State sum models with defects
Catherine Meusburger University of Erlangen-Nuremberg
-

Quantum information and black holes
Johanna Erdmenger University of Würzburg
-

Researcher Presentations
-
Karen Yeats University of Waterloo
-
Sabine Harribey Dublin Institute For Advanced Studies
-
Philine van Vliet Deutsches Elektronen-Synchrotron DESY
-
Maria Elena Tejeda-Yeomans University of Colima
-
Maryam Khaqan Emory University
-
-

Mathematical Puzzles from Causal Set Quantum Gravity
Sumati Surya Raman Research Institute
-

On generalized hyperpolygons
Laura Schaposnik University of Illinois at Chicago
-

Exploring spacetime beyond classicality
Renate Loll Radboud Universiteit Nijmegen
-
-
Mathematical Physics (Elective), PHYS 777, March 31 - May 2, 2025
13 talks-Collection NumberC25007We will discuss mathematical aspects of classical and quantum field theory, including topics such as: symplectic manifolds and the phase space, symplectic reduction, geometric quantization, Chern-Simons theory, and others. Instructor: Kevin Costello/Mykola Semenyakin Students who are not part of the PSI MSc program should review enrollment and course format information here: https://perimeterinstitute.ca/graduate-courses -
Mathematical Physics (Core), PHYS 777-, January 6 - February 5, 2025
13 talks-Collection NumberC25002This course will introduce you to some of the geometrical structures underlying theoretical physics. Previous knowledge of differential geometry is not required. Topics covered in the course include: Introduction to manifolds, differential forms, symplectic manifolds, symplectic version of Noether’s theorem, integration on manifolds, fiber bundles, principal bundles and applications to gauge theory. Instructor: Mykola Semenyakin/Maite Dupuis Students who are not part of the PSI MSc program should review enrollment and course format information here: https://perimeterinstitute.ca/graduate-courses -
Classical Physics (Core), PHYS 776, September 3 - October 4, 2024
15 talks-Collection NumberC24031This is a theoretical physics course that aims to review the basics of theoretical mechanics, special relativity, and classical field theory, with the emphasis on geometrical notions and relativistic formalism, thus setting the stage for the forthcoming courses in Quantum Mechanics, and Quantum Field Theory in particular, as well as in General Relativity and Quantum Gravity. Instructor: Aldo Riello Students who are not part of the PSI MSc program should review enrollment and course format information here: https://perimeterinstitute.ca/graduate-courses -
Mathematical Physics 2023/24
13 talks-Collection NumberC24026We will discuss mathematical aspects of classical and quantum field theory, including topics such as: symplectic manifolds and the phase space, symplectic reduction, geometric quantization, Chern-Simons theory, and others. -
Higher Categorical Tools for Quantum Phases of Matter
15 talks-Collection NumberC24016Quantum phases have become a staple of modern physics, thanks to their appearance in fields as diverse as condensed matter physics, quantum field theory, quantum information processing, and topology. The description of quantum phases of matter requires novel mathematical tools that lie beyond the old symmetry breaking perspective on phases. Techniques from topological field theory, homotopy theory, and (higher) category theory show great potential for advancing our understanding of the characterization and classification of quantum phases. The goal of this workshop is to bring together experts from across mathematics and physics to discuss recent breakthroughs in these mathematical tools and their application to physical problems.
Scientific Organizers
Lukas Mueller
Alex Turzillo
Davide Gaiotto
Sponsored in part by the Simons Collaboration on Global Categorical Symmetries

-
Quantum Field Theory for Cosmology (PHYS785/AMATH872)
24 talks-Collection NumberC24003This course introduces quantum field theory from scratch and then develops the theory of the quantum fluctuations of fields and particles. We will focus, in particular, on how quantum fields are affected by curvature and by spacetime horizons. This will lead us to the Unruh effect, Hawking radiation and to inflationary cosmology. Inflationary cosmology, which we will study in detail, is part of the current standard model of cosmology which holds that all structure in the universe - such as the distribution of galaxies - originated in tiny quantum fluctuations of a scalar field and of space-time itself. For intuition, consider that quantum field fluctuations of significant amplitude normally occur only at very small length scales. Close to the big bang, during a brief initial period of nearly exponentially fast expansion (inflation), such small-wavelength but large-amplitude quantum fluctuations were stretched out to cosmological wavelengths. In this way, quantum fluctuations are thought to have seeded the observed inhomogeneities in the cosmic microwave background - which in turn seeded the condensation of hydrogen into galaxies and stars, all closely matching the increasingly accurate astronomical observations over recent years. The prerequisites for this course are a solid understanding of quantum theory and some basic knowledge of general relativity, such as FRW spacetimes.
https://uwaterloo.ca/physics-of-information-lab/teaching/quantum-field-theory-cosmology-amath872phys785-w2024
https://pitp.zoom.us/j/96567241418?pwd=U3I1V1g4YXdaZ3psT1FrZUdlYm1zdz09
-
Mathematical Physics - Core 2023/24
12 talks-Collection NumberC24005This course will introduce you to some of the geometrical structures underlying theoretical physics. Previous knowledge of differential geometry is not required. Topics covered in the course include: Introduction to manifolds, differential forms, symplectic manifolds, symplectic version of Noether’s theorem, integration on manifolds, fiber bundles, principal bundles and applications to gauge theory.
-
Twisted Holography Mini-Course
6 talks-Collection NumberC23050This mini-course will introduce twisted holography, which is holography for BPS subsectors of gauge theory and gravity. We will start by introducing the B-model topological string from the space-time perspective, before discussing branes, backreaction, and the holographic duality.
Zoom: https://pitp.zoom.us/j/98839130613?pwd=SExFK0ZVYzJ3NmJhU1RFa21PWU1qQT09
-
Topological Quantum Field Theories - mini-course
9 talks-Collection NumberC23048A quantum field theory is deemed topological if it exhibits the remarkable property of being independent of any background metric. In contrast to most other types of quantum field theories, topological quantum field theories possess a well-defined mathematical framework, tracing its roots back to the pioneering work of Atiyah in 1988. The mathematical tools employed to define and study topological quantum field theories encompass concepts from category theory, homotopy theory, topology, and algebra.
In this course, we will delve into the mathematical foundations of this field, explore examples and classification results, especially in lower dimensions. Subsequently, we will explore more advanced aspects, such as invertible theories, defects, the cobordism hypothesis, or state sum models in dimensions 3 and 4 (including Turaev-Viro and Douglas-Reutter models), depending on the interests of the audience.
Today, the mathematics of topological quantum field theories has found numerous applications in physics. Recent applications include the study of anomalies, non-invertible symmetries, the classification of topological phases of matter, and lattice models. The course aims to provide the necessary background for understanding these applications. -
-
-
Women at the Intersection of Mathematics and Theoretical Physics
16 talks-Collection NumberC21002