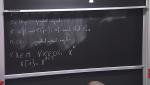Hitchin Systems in Mathematics and Physics
18
talks
-
Collection NumberC17001
Mathematical physics, including mathematics, is a research area where novel mathematical techniques are invented to tackle problems in physics, and where novel mathematical ideas find an elegant physical realization. Historically, it would have been impossible to distinguish between theoretical physics and pure mathematics. Often spectacular advances were seen with the concurrent development of new ideas and fields in both mathematics and physics. Here one might note Newton's invention of modern calculus to advance the understanding of mechanics and gravitation. In the twentieth century, quantum theory was developed almost simultaneously with a variety of mathematical fields, including linear algebra, the spectral theory of operators and functional analysis. This fruitful partnership continues today with, for example, the discovery of remarkable connections between gauge theories and string theories from physics and geometry and topology in mathematics.
Displaying 25 - 36 of 896
Format results
-
Talk
-
Critical points and spectral curves
Nigel Hitchin University of Oxford
-
Generalizing Quivers: Bows, Slings, Monowalls
Sergey Cherkis University of Arizona
-
-
Nahm transformation for parabolic harmonic bundles on the projective line with regular residues
Szilard Szabo Budapest University of Technology and Economics
-
A mathematical definition of 3d indices
Tudor Dimofte University of Edinburgh
-
Perverse Hirzebruch y-genus of Higgs moduli spaces
Tamas Hausel Institute of Science and Technology Austria
-
Motivic Classes for Moduli of Connections
Alexander Soibelman University of Southern California
-
BPS algebras and twisted character varieties
Ben Davison University of Edinburgh
-
-
Deformation Quantization of Shifted Poisson Structures
17 talks-Collection NumberC16005Talk
-
Formal derived stack and Formal localization
Michel Vaquie Laboratoire de Physique Théorique, IRSAMC, Université Paul Sabatier
-
An overview of derived analytic geometry
Mauro Porta Institut de Mathématiques de Jussieu
-
Categorification of shifted symplectic geometry using perverse sheaves
Dominic Joyce University of Oxford
-
Shifted structures and quantization
Tony Pantev University of Pennsylvania
-
What is the Todd class of an orbifold?
Andrei Caldararu University of Wisconsin–Madison
-
Singular support of categories
Dima Arinkin University of Wisconsin-Milwaukee
-
Symplectic and Lagrangian structures on mapping stacks
Theodore Spaide Universität Wien
-
The Maslov cycle and the J-homomorphism
David Treumann Boston College
-
-
Mathematica Summer School
18 talks-Collection NumberC15040Talk
-
Welcome to “Mathematica Summer School”
Pedro Vieira Perimeter Institute for Theoretical Physics
-
Mathematica School Lecture - 2015
Horacio Casini Bariloche Atomic Centre
-
Quantum mechanics in the early universe
Juan Maldacena Institute for Advanced Study (IAS) - School of Natural Sciences (SNS)
-
-
Ground state entanglement and tensor networks
Guifre Vidal Alphabet (United States)
-
Quantum mechanics in the early universe
Juan Maldacena Institute for Advanced Study (IAS) - School of Natural Sciences (SNS)
-
Mathematica School Lecture - 2015
Pedro Vieira Perimeter Institute for Theoretical Physics
-
Holographic entanglement entropy
Robert Myers Perimeter Institute for Theoretical Physics
-
-
Lecture - Mathematical Physics, PHYS 777
Mykola Semenyakin Perimeter Institute for Theoretical Physics
-
-
Ideas in Multiplicative Non-abelian Hodge theory
Marielle Ong University of Toronto
-
The sewing-factorization theorem for $C_2$-cofinite VOAs
Hao Zhang Tsinghua University
-
Matroids and the Moduli Space of Abelian Varieties
Juliette Bruce Dartmouth College
-
Graphs, curves, and their moduli spaces (Part 2 of 2)
Michael Borinsky Perimeter Institute for Theoretical Physics
-
-
Graphs, curves, and their moduli spaces (Part 1 of 2)
Michael Borinsky Perimeter Institute for Theoretical Physics
-
-
Hitchin Systems in Mathematics and Physics
18 talks-Collection NumberC17001Hitchin Systems in Mathematics and Physics
-
Deformation Quantization of Shifted Poisson Structures
17 talks-Collection NumberC16005Deformation Quantization of Shifted Poisson Structures
-
-
Lecture - Mathematical Physics, PHYS 777
Mykola Semenyakin Perimeter Institute for Theoretical Physics
-
-
Ideas in Multiplicative Non-abelian Hodge theory
Marielle Ong University of Toronto
Non-abelian Hodge theory is a profound three-way equivalence between topological, smooth and holomorphic objects, i.e. representations of the fundamental group, flat connections and Higgs bundles. It is natural to explore a group-theoretic or multiplicative version — an enterprise that has been untaken by Soibelman, Kontsevich, Mochizuki and others. In this talk, we will review the current landscape of multiplicative non-abelian Hodge theory and discuss some outstanding questions. -
The sewing-factorization theorem for $C_2$-cofinite VOAs
Hao Zhang Tsinghua University
In this talk, I will present a sewing-factorization theorem for conformal blocks in arbitrary genus associated to a (possibly nonrational) $C_2$-cofinite VOA $V$. This result gives a higher genus analog of Huang-Lepowsky-Zhang's tensor product theory. Moreover, I will explain the relation between our result and pseudotraces, and confirm some of the conjectures by Gainuditnov-Runkel. The relationship between our result and coends will also be discussed. The talk is based on an ongoing project (arXiv: 2305.10180, 2411.07707) joint with Bin Gui.
-
Matroids and the Moduli Space of Abelian Varieties
Juliette Bruce Dartmouth College
Inspired by recent work calculating the top weight cohomology of the moduli space $\mathcal{A}_g$ of principally polarized abelian varieties of dimension $g$ for small values of $g$, I will discuss a connection between matroids and compactifications of $\mathcal{A}_g$ that is anlogous to the connection between graphs and compactifications of the moduli space of curves. Given time I will also discuss recent work computing the homology of various matroid complexes. -
Graphs, curves, and their moduli spaces (Part 2 of 2)
Michael Borinsky Perimeter Institute for Theoretical Physics
I will give a gentle introduction to the moduli space of graphs and its fine moduli space cousin known as Outer Space. This moduli space of graphs has many applications to various branches of mathematical physics, algebraic geometry, and geometric group theory. It is a natural object to consider while studying Feynman amplitudes in parametric space, and it can be seen as the configuration space of one-dimensional quantum gravity. I will explain how this moduli space of graphs recently became the largest provider of information on the homology of the moduli space of curves of genus g and how associated graph complexes can be used to shed light on the 'dark-matter problems' of these moduli space's cohomology. -
Heun operator and Bethe ansatz
After an introduction to the notion of Leonard pairs, I explain their different uses. Then, I provide the definition of the associated Heun operator and how it allows us to simplify the computation of the quantum entanglement entropy. Finally, I show, in the simplest example, how the Bethe ansatz can be used to diagonalize the Heun operator.
-
Graphs, curves, and their moduli spaces (Part 1 of 2)
Michael Borinsky Perimeter Institute for Theoretical Physics
I will give a gentle introduction to the moduli space of graphs and its fine moduli space cousin known as Outer Space. This moduli space of graphs has many applications to various branches of mathematical physics, algebraic geometry, and geometric group theory. It is a natural object to consider while studying Feynman amplitudes in parametric space, and it can be seen as the configuration space of one-dimensional quantum gravity. I will explain how this moduli space of graphs recently became the largest provider of information on the homology of the moduli space of curves of genus g and how associated graph complexes can be used to shed light on the 'dark-matter problems' of these moduli space's cohomology. -
Dynamical Yangians of cotangent Lie algebras over moduli spaces of G-bundles
Raschid AbedinIn this talk, I will present the construction of the Yangian of a cotangent Lie algebra from the geometry of the equivariant affine Grassmannian. Furthermore, I will discuss how this quantum group can be dynamically twisted to a quantum groupoid over a neighborhood in the moduli space of G-bundles over a compact Riemann surface. These constructions are motivated by relations between a certain holomorphic-topological 4d gauge field theory and the geometric Langlands correspondence. Representations of the Yangian are pertubative line operators of said theory, while the dynamical twist of the Yangian controls the action of these operators via Hecke modifications in this setting. This talk is based on the two joint works arXiv:2405.19906 and arXiv:2411.05068 with Wenjun Niu.