Talks by Howard Barnum
Entropy, majorization, and thermodynamics in general probabilistic theories.
Howard Barnum University of New Mexico
Generalizations of Quantum Theory
-
Lucien Hardy Perimeter Institute for Theoretical Physics
-
Rafael Sorkin Perimeter Institute for Theoretical Physics
-
Wayne Myrvold Western University
-
Howard Barnum University of New Mexico
-
Joe Henson Evince Asset Management LP
-
Markus Mueller Institute for Quantum Optics and Quantum Information (IQOQI) - Vienna
Composite systems and information processing
Howard Barnum University of New Mexico
Probabilities from Quantum States, or Quantum States from Probabilities?
Howard Barnum University of New Mexico
Jordan algebras and spectrality as tools for axiomatic characterization
Howard Barnum University of New Mexico
Convex and Categorial Frameworks for Information Processing and Physics
Howard Barnum University of New Mexico
SICs, Convex Cones, and Algebraic Sets
Howard Barnum University of New Mexico
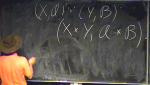
Nonlocal no-signalling correlations that are locally quantum.
Howard Barnum University of New Mexico