
Lie superalgebras and S-duality
Alexander Braverman University of Toronto

Alexander Braverman University of Toronto

David Ben-Zvi The University of Texas at Austin

David Ben-Zvi The University of Texas at Austin

Davide Gaiotto Perimeter Institute for Theoretical Physics
Lotte Hollands Heriot-Watt University
Joerg Teschner Deutsches Elektronen-Synchrotron DESY
Fei Yan Rutgers University

Lotte Hollands Heriot-Watt University

Lotte Hollands Heriot-Watt University
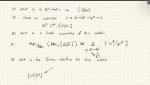
Tudor Dimofte University of Edinburgh
Benjamin Gammage Harvard University
Ahsan Khan Institute for Advanced Study (IAS)

Benjamin Gammage Harvard University

Davide Gaiotto Perimeter Institute for Theoretical Physics
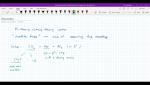
Tudor Dimofte University of Edinburgh
Lev Rozansky University of North Carolina at Chapel Hill
Ben Webster University of Waterloo

Fei Yan Rutgers University

Joerg Teschner Deutsches Elektronen-Synchrotron DESY