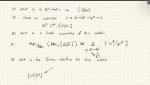Discussion on 4d N=2
-
Davide Gaiotto Perimeter Institute for Theoretical Physics
-
Lotte Hollands Heriot-Watt University
-
Joerg Teschner Deutsches Elektronen-Synchrotron DESY
-
Fei Yan Rutgers University