
Displaying 4549 - 4560 of 5164
Format results
-

-

Meson widths from string worldsheet instantons.
Thomas Faulkner University of Illinois Urbana-Champaign
-

Explaining Regularities: The Need for Singular Behaviour
Bob Batterman University of Pittsburgh
-
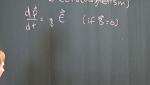
Gravitoelectromagnetism
Edmund Bertschinger Massachusetts Institute of Technology (MIT) - Department of Physics
-

-

Measurement Pattern Interpolation: Theory, and potential applications
Niel de Beaudrap Institute for Quantum Computing (IQC)
-

What is a Wavefunction?
Garnet Ord Toronto Metropolitan University
-

-
Non-conformal holography
Kostas Skenderis University of Southampton
-

Clustering in interacting dark energy cosmologies
Valeria Pettorino Universität Heidelberg
-

Statistical Prediction of the Outcome of a Noncooperative Game
David Wolpert National Aeronautics and Space Administration
-

Finite States in Four Dimensional Quantized Gravity
Eyo Ita US Naval Academy and Cambridge University (DAMTP)