
Displaying 4525 - 4536 of 5164
Format results
-

-

-
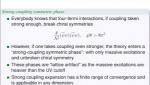
Lattice chirality: a mission (im)possible?
Yanwen Shang Citigroup Incorporated
-

Constraint free canonical GR using characteristic data
Michael Reisenberger Universidad de la Republica Uruguay
-

Quantum Non-Booleanity, Simultaneity and the Despatialization of Time
Kent Peacock University of Lethbridge
-

Quantum and Thermal decay in de Sitter space
Adam Brown Stanford University
-

-

-

-

-

Why there is no information loss
Abhay Ashtekar Pennsylvania State University
-
