Format results
-
13 talks-Collection NumberC24023
Talk
-

Strong Gravity Lecture
William East Perimeter Institute for Theoretical Physics
-

Strong Gravity Lecture
William East Perimeter Institute for Theoretical Physics
-

Strong Gravity Lecture
William East Perimeter Institute for Theoretical Physics
-

Strong Gravity Lecture
William East Perimeter Institute for Theoretical Physics
-

Strong Gravity Lecture
William East Perimeter Institute for Theoretical Physics
-

Strong Gravity Lecture
William East Perimeter Institute for Theoretical Physics
-

Strong Gravity Lecture
William East Perimeter Institute for Theoretical Physics
-

Strong Gravity Lecture
William East Perimeter Institute for Theoretical Physics
-
-
String Theory 2023/24
13 talks-Collection NumberC24025Talk
-

String Theory Lecture
Davide Gaiotto Perimeter Institute for Theoretical Physics
-

String Theory Lecture
Davide Gaiotto Perimeter Institute for Theoretical Physics
-

String Theory Lecture
Davide Gaiotto Perimeter Institute for Theoretical Physics
-

String Theory Lecture
Davide Gaiotto Perimeter Institute for Theoretical Physics
-

String Theory Lecture
Davide Gaiotto Perimeter Institute for Theoretical Physics
-

String Theory Lecture
Davide Gaiotto Perimeter Institute for Theoretical Physics
-

String Theory Lecture
Davide Gaiotto Perimeter Institute for Theoretical Physics
-

String Theory Lecture
Davide Gaiotto Perimeter Institute for Theoretical Physics
-
-
Machine Learning 2023/24
12 talks-Collection NumberC24027Talk
-

Machine Learning Lecture
Mohamed Hibat Allah University of Waterloo
-

Machine Learning Lecture
Mohamed Hibat Allah University of Waterloo
-

Machine Learning Lecture
Mohamed Hibat Allah University of Waterloo
-

Machine Learning Lecture
Mohamed Hibat Allah University of Waterloo
-

Machine Learning Lecture
Mohamed Hibat Allah University of Waterloo
-

Machine Learning Lecture
Mohamed Hibat Allah University of Waterloo
-

Machine Learning Lecture
Mohamed Hibat Allah University of Waterloo
-

Machine Learning Lecture
Mohamed Hibat Allah University of Waterloo
-
-
Quantum Gravity 2023/24
13 talks-Collection NumberC24024Talk
-

Quantum Gravity Lecture
Aldo Riello Perimeter Institute for Theoretical Physics
-

Quantum Gravity Lecture
Aldo Riello Perimeter Institute for Theoretical Physics
-

Quantum Gravity Lecture
Aldo Riello Perimeter Institute for Theoretical Physics
-

Quantum Gravity Lecture
Aldo Riello Perimeter Institute for Theoretical Physics
-

Quantum Gravity Lecture
Aldo Riello Perimeter Institute for Theoretical Physics
-

Quantum Gravity Lecture
Aldo Riello Perimeter Institute for Theoretical Physics
-

Quantum Gravity Lecture
Aldo Riello Perimeter Institute for Theoretical Physics
-

Quantum Gravity Lecture
Aldo Riello Perimeter Institute for Theoretical Physics
-
-
GPTs and the probabilistic foundations of quantum theory - mini-course
7 talks-Collection NumberC24021Talk
-

GPTs and the probabilistic foundations of quantum theory - Lecture
Alexander Wilce Susquehanna University
-

GPTs and the probabilistic foundations of quantum theory - Lecture
Alexander Wilce Susquehanna University
-

GPTs and the probabilistic foundations of quantum theory - Lecture
Alexander Wilce Susquehanna University
-

GPTs and the probabilistic foundations of quantum theory - Lecture
Alexander Wilce Susquehanna University
-

GPTs and the probabilistic foundations of quantum theory - Lecture
Alexander Wilce Susquehanna University
-

GPTs and the probabilistic foundations of quantum theory - Lecture
Alexander Wilce Susquehanna University
-

GPTs and the probabilistic foundations of quantum theory - Lecture
Alexander Wilce Susquehanna University
-
-
Quantum Information 2023/24
13 talks-Collection NumberC24012Talk
-

Quantum Information Lecture
Eduardo Martin-Martinez University of Waterloo
-

Quantum Information Lecture
Eduardo Martin-Martinez University of Waterloo
-

Quantum Information Lecture
Eduardo Martin-Martinez University of Waterloo
-

Quantum Information Lecture
Eduardo Martin-Martinez University of Waterloo
-

Quantum Information Lecture
Eduardo Martin-Martinez University of Waterloo
-

Quantum Information Lecture
Eduardo Martin-Martinez University of Waterloo
-

Quantum Information Lecture
Eduardo Martin-Martinez University of Waterloo
-

Quantum Information Lecture
Eduardo Martin-Martinez University of Waterloo
-
-
Particle Physics
12 talks-Collection NumberC24009Talk
-

Particle Physics Lecture
Asimina Arvanitaki Perimeter Institute for Theoretical Physics
-
Particle Physics Lecture
Asimina Arvanitaki Perimeter Institute for Theoretical Physics
-

Particle Physics Lecture
Asimina Arvanitaki Perimeter Institute for Theoretical Physics
-

Particle Physics Lecture
Asimina Arvanitaki Perimeter Institute for Theoretical Physics
-

Particle Physics Lecture
Asimina Arvanitaki Perimeter Institute for Theoretical Physics
-

Particle Physics Lecture
Asimina Arvanitaki Perimeter Institute for Theoretical Physics
-

Particle Physics Lecture
Junwu Huang Perimeter Institute for Theoretical Physics
-

Particle Physics Lecture
Junwu Huang Perimeter Institute for Theoretical Physics
-
-
QFT III 2023/24
13 talks-Collection NumberC24010Talk
-

QFT III Lecture
Jaume Gomis Perimeter Institute for Theoretical Physics
-

QFT III Lecture
Jaume Gomis Perimeter Institute for Theoretical Physics
-

QFT III Lecture
Jaume Gomis Perimeter Institute for Theoretical Physics
-

QFT III Lecture
Jaume Gomis Perimeter Institute for Theoretical Physics
-

QFT III Lecture
Jaume Gomis Perimeter Institute for Theoretical Physics
-

QFT III Lecture
Mykola Semenyakin Perimeter Institute for Theoretical Physics
-

QFT III Lecture
Mykola Semenyakin Perimeter Institute for Theoretical Physics
-

QFT III Lecture
Mykola Semenyakin Perimeter Institute for Theoretical Physics
-
-
Quantum Matter 2023/24
13 talks-Collection NumberC24011Talk
-

Quantum Matter Lecture
Timothy Hsieh Perimeter Institute for Theoretical Physics
-

Quantum Matter Lecture
Timothy Hsieh Perimeter Institute for Theoretical Physics
-

Quantum Matter Lecture
Timothy Hsieh Perimeter Institute for Theoretical Physics
-

-

-

-

-

-
-
Cosmology 2023/24
13 talks-Collection NumberC24013Talk
-

Cosmology Lecture
Kendrick Smith Perimeter Institute for Theoretical Physics
-

Cosmology Lecture
Kendrick Smith Perimeter Institute for Theoretical Physics
-

Cosmology Lecture
Kendrick Smith Perimeter Institute for Theoretical Physics
-

Cosmology Lecture
Kendrick Smith Perimeter Institute for Theoretical Physics
-

Cosmology Lecture
Kendrick Smith Perimeter Institute for Theoretical Physics
-

Cosmology Lecture
Kendrick Smith Perimeter Institute for Theoretical Physics
-

Cosmology Lecture
Kendrick Smith Perimeter Institute for Theoretical Physics
-

Cosmology Lecture
Kendrick Smith Perimeter Institute for Theoretical Physics
-
-
Advanced General Relativity (PHYS7840)
24 talks-Collection NumberC24001Talk
-
Quantum Field Theory for Cosmology (PHYS785/AMATH872)
24 talks-Collection NumberC24003Talk
-

Quantum Field Theory for Cosmology - Lecture 20240109
Achim Kempf University of Waterloo
-
Quantum Field Theory for Cosmology - Lecture 20240111
Achim Kempf University of Waterloo
-

Quantum Field Theory for Cosmology - Lecture 20240116
Achim Kempf University of Waterloo
-

Quantum Field Theory for Cosmology - Lecture 20240118
Achim Kempf University of Waterloo
-

Quantum Field Theory for Cosmology - Lecture 20240123
Achim Kempf University of Waterloo
-

Quantum Field Theory for Cosmology - Lecture 20240125
Achim Kempf University of Waterloo
-

Quantum Field Theory for Cosmology - Lecture 20240130
Achim Kempf University of Waterloo
-

Quantum Field Theory for Cosmology - Lecture 20240201
Achim Kempf University of Waterloo
-
-
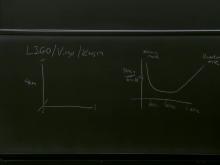
Strong Gravity 2023/24
13 talks-Collection NumberC24023This course will introduce some advanced topics in general relativity related to describing gravity in the strong field and dynamical regime. Topics covered include properties of spinning black holes, black hole thermodynamics and energy extraction, how to define horizons in a dynamical setting, formulations of the Einstein equations as constraint and evolution equations, and gravitational waves and how they are sourced. -
String Theory 2023/24
13 talks-Collection NumberC24025The course covers the basics of String Theory: bosonic strings, D-branes, a bit of superstrings.
-
Machine Learning 2023/24
12 talks-Collection NumberC24027Machine learning has become a very valuable toolbox for scientists including physicists. In this course, we will learn the basics of machine learning with an emphasis on applications for many-body physics. At the end of this course, you will be equipped with the necessary and preliminary tools for starting your own machine learning projects. -
Quantum Gravity 2023/24
13 talks-Collection NumberC24024The course centers on an in-depth study of the symmetry structure of General Relativity and how this is intimately related to its dynamics and to the challenges posed to its quantization. To achieve this understanding, we will introduce a host of concepts and techniques, broadly (and loosely) known under the name of “Covariant Phase Space Method”. This provides a different perspective on GR’s physics, a perspective in which phase space, rather than spacetime, is front and center. We will apply these ideas and techniques to discuss the so-called Problem of Time, Wald's approach to black hole entropy as a Noether charge, and the relationship between Dirac's Hypersurface Deformation Algebra and GR's symmetries and dynamics. We will also discuss the problem of detecting single gravitons as well as crucial analogies and differences between a quantum electromagnetic and gravitational field. Lecture notes specific for the course will be provided. -
GPTs and the probabilistic foundations of quantum theory - mini-course
7 talks-Collection NumberC24021Classical probability theory makes the (mostly, tacit) assumption that any two random experiments can be performed jointly. This assumption seems to fail in quantum theory. A rapidly growing literature seeks to understand QM by placing it in a much broader mathematical landscape of ``generalized probabilistic theories", or GPTs, in which incompatible experiments are permitted. Among other things, this effort has led to (i) a better appreciation that many "characteristically quantum" phenomena (e.g., entanglement) are in fact generic to non-classical probabilistic theories, (ii) a suite of reconstructions of (mostly, finite-dimensional) QM from small packages of assumptions of a probabilistic or operational nature, and (iii) a clearer view of the options available for generalizing QM. This course will offer a survey of this literature, starting from scratch and concluding with a discussion of recent developments.
Mathematical prerequisites: finite-dimensional linear algebra, ideally including tensor products and duality, plus some exposure to category theory (though I will briefly review this material as needed).
Scheduling note: There will be 5 lectures from March 12-26, then a gap of two weeks before the final 2 lectures held April 16 & 18.
Format: In-person only; lectures will be recorded for PIRSA but not live on Zoom.
-
-
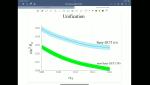
Particle Physics
12 talks-Collection NumberC24009This course will cover phenomenological studies and experimental searches for new physics beyond the Standard Model, including: naturalness, extra dimension, supersymmetry, grand unification, dark matter candidates (WIMPs and axions) and their detection.
-
QFT III 2023/24
13 talks-Collection NumberC24010This survey course introduces some advanced topics in quantum field theory and string theory. Topics may include anomalies, conformal field theory, and bosonic string theory and are subject to change depending on the topics covered in the TBD elective course.
-
Quantum Matter 2023/24
13 talks-Collection NumberC24011This course will cover quantum phases of matter, with a focus on long-range entangled states, topological states, and quantum criticality.
-
Cosmology 2023/24
13 talks-Collection NumberC24013This Cosmology course will provide a theoretical overview of the standard cosmological model.
Topics will include: FRW universe, Thermal History, Inflation, Cosmological Perturbation Theory, Structure Formation and Quantum Initial Conditions. -
Advanced General Relativity (PHYS7840)
24 talks-Collection NumberC24001Review of elementary general relativity. Timelike and null geodesic congruences. Hypersurfaces and junction conditions. Lagrangian and Hamiltonian formulations of general relativity. Mass and angular momentum of a gravitating body. The laws of black-hole mechanics.
Zoom: https://pitp.zoom.us/j/97183751661?pwd=T0szNnRjdUM2dENYNTdmRmJCZVF1QT09
-
Quantum Field Theory for Cosmology (PHYS785/AMATH872)
24 talks-Collection NumberC24003This course introduces quantum field theory from scratch and then develops the theory of the quantum fluctuations of fields and particles. We will focus, in particular, on how quantum fields are affected by curvature and by spacetime horizons. This will lead us to the Unruh effect, Hawking radiation and to inflationary cosmology. Inflationary cosmology, which we will study in detail, is part of the current standard model of cosmology which holds that all structure in the universe - such as the distribution of galaxies - originated in tiny quantum fluctuations of a scalar field and of space-time itself. For intuition, consider that quantum field fluctuations of significant amplitude normally occur only at very small length scales. Close to the big bang, during a brief initial period of nearly exponentially fast expansion (inflation), such small-wavelength but large-amplitude quantum fluctuations were stretched out to cosmological wavelengths. In this way, quantum fluctuations are thought to have seeded the observed inhomogeneities in the cosmic microwave background - which in turn seeded the condensation of hydrogen into galaxies and stars, all closely matching the increasingly accurate astronomical observations over recent years. The prerequisites for this course are a solid understanding of quantum theory and some basic knowledge of general relativity, such as FRW spacetimes.
https://uwaterloo.ca/physics-of-information-lab/teaching/quantum-field-theory-cosmology-amath872phys785-w2024
https://pitp.zoom.us/j/96567241418?pwd=U3I1V1g4YXdaZ3psT1FrZUdlYm1zdz09