
Bipartite states of low rank are almost surely entangled
Mary Beth Ruskai University of Massachusetts Lowell

Mary Beth Ruskai University of Massachusetts Lowell

Christoph Stephan University of Potsdam


Mark Wyman PDT Partners LLC
Niayesh Afshordi University of Waterloo

Henry Haselgrove Defence Science and Technology Group
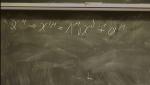



Rene Meyer Max-Planck Gesellschaft

Cameron Neylon University of Southampton

