
Displaying 3289 - 3300 of 5164
Format results
-

-

À la recherche du temps perdu - Templeton Frontiers Colloquia
Flavio Mercati University of Naples Federico II
-

Numerical detection of symmetry protected and symmetry enriched topological phases
Frank Pollmann Max Planck Institute for Physics, Munich (Werner-Heisenberg-Institut)
-

Large Tensor-to-Scalar Ratio in Small-Field Inflation
Takeshi Kobayashi SISSA International School for Advanced Studies
-

Probing the Small Scale Structure of Dark Matter with Indirect Detection
Sheldon Campbell Ohio State University
-

Quantum Liquids and Turbulent Black Holes
Allan Adams Massachusetts Institute of Technology (MIT) - Department of Physics
-
-
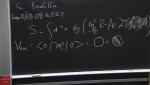
Sequestering the Standard Model Vacuum Energy
Nemanja Kaloper University of California, Davis
-

-

The Sherrington-Kirkpatrick model and its diluted version
Dmitry Panchenko Texas A&M University
-

-

The emergent of the chiral spin liquid in kagome Heisenberg model
Dong-Ning Sheng California State University, Northridge