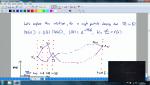
11977 - 11988 of 16889 Results
Format results


Building Fractional Topological Insulators
Fiona Burnell University of Minnesota

A Natural Language for AdS/CFT Correlators
Joao Penedones L'Ecole Polytechnique Federale de Lausanne (EPFL)

Integral Transforms and Green's Functions - Lecture 4
David Kubiznak Charles University

Special Functions and Distributions - Lecture 4
Dan Wohns Perimeter Institute for Theoretical Physics

Cosmology Meets Quantum Gravity: a Chiral Signature in the CMB?
Joao Magueijo Imperial College London